support vector machine (SVM)

What is a support vector machine (SVM)?

A support vector machine (SVM) is a type of supervised learning algorithm used in machine learning to solve classification and regression tasks; SVMs are particularly good at solving binary classification problems, which require classifying the elements of a data set into two groups.

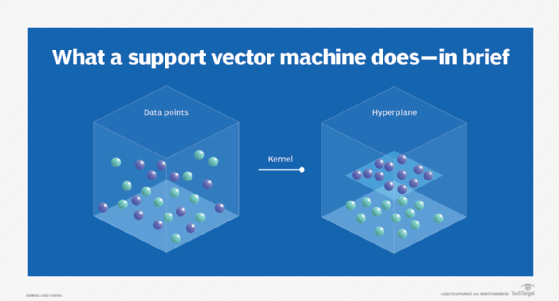
The aim of a support vector machine algorithm is to find the best possible line, or decision boundary, that separates the data points of different data classes. This boundary is called a hyperplane when working in high-dimensional feature spaces. The idea is to maximize the margin, which is the distance between the hyperplane and the closest data points of each category, thus making it easy to distinguish data classes.

SVMs are useful for analyzing complex data that can't be separated by a simple straight line. Called nonlinear SMVs, they do this by using a mathematical trick that transforms data into higher-dimensional space, where it is easier to find a boundary.

How do support vector machines work?

The key idea behind SVMs is to transform the input data into a higher-dimensional feature space. This transformation makes it easier to find a linear separation or to more effectively classify the data set.

To do this, SVMs use a kernel function. Instead of explicitly calculating the coordinates of the transformed space, the kernel function enables the SVM to implicitly compute the dot products between the transformed feature vectors and avoid handling expensive, unnecessary computations for extreme cases.

SVMs can handle both linearly separable and non-linearly separable data. They do this by using different types of kernel functions, such as the linear kernel, polynomial kernel or radial basis function (RBF) kernel. These kernels enable SVMs to effectively capture complex relationships and patterns in the data.

During the training phase, SVMs use a mathematical formulation to find the optimal hyperplane in a higher-dimensional space, often called the kernel space. This hyperplane is crucial because it maximizes the margin between data points of different classes, while minimizing the classification errors.

The kernel function plays a critical role in SVMs, as it makes it possible to map the data from the original feature space to the kernel space. The choice of kernel function can have a significant impact on the performance of the SVM algorithm; choosing the best kernel function for a particular problem depends on the characteristics of the data.

Some of the most popular kernel functions for SVMs are the following:

• Linear kernel. This is the simplest kernel function, and it maps the data to a higher-dimensional space, where the data is linearly separable.
• Polynomial kernel. This kernel function is more powerful than the linear kernel, and it can be used to map the data to a higher-dimensional space, where the data is non-linearly separable.
• RBF kernel. This is the most popular kernel function for SVMs, and it is effective for a wide range of classification problems.
• Sigmoid kernel. This kernel function is similar to the RBF kernel, but it has a different shape that can be useful for some classification problems.

The choice of kernel function for an SVM algorithm is a tradeoff between accuracy and complexity. The more powerful kernel functions, such as the RBF kernel, can achieve higher accuracy than the simpler kernel functions, but they also require more data and computation time to train the SVM algorithm. But this is becoming less of an issue due to technological advances.

Once trained, SVMs can classify new, unseen data points by determining which side of the decision boundary they fall on. The output of the SVM is the class label associated with the side of the decision boundary.

Types of support vector machines

Support vector machines have different types and variants that provide specific functionalities and address specific problem scenarios. Here are two types of SVMs and their significance:

1. Linear SVM. Linear SVMs use a linear kernel to create a straight-line decision boundary that separates different classes. They are effective when the data is linearly separable or when a linear approximation is sufficient. Linear SVMs are computationally efficient and have good interpretability, as the decision boundary is a hyperplane in the input feature space.
2. Nonlinear SVM. Nonlinear SVMs address scenarios where the data cannot be separated by a straight line in the input feature space. They achieve this by using kernel functions that implicitly map the data into a higher-dimensional feature space, where a linear decision boundary can be found. Popular kernel functions used in this type of SVM include the polynomial kernel, Gaussian (RBF) kernel and sigmoid kernel. Nonlinear SVMs can capture complex patterns and achieve higher classification accuracy when compared to linear SVMs.

Advantages of SVMs

SVMs are powerful machine learning algorithms that have the following advantages:

• Effective in high-dimensional spaces. High-dimensional data refers to data in which the number of features is larger than the number of observations, i.e., data points. SVMs perform well even when the number of features is larger than the number of samples. They can handle high-dimensional data efficiently, making them suitable for applications with a large number of features.
• Resistant to overfitting. SVMs are less prone to overfitting compared to other algorithms, like decision trees -- overfitting is where a model performs extremely well on the training data but becomes too specific to that data and can't generalize to new data. SVMs' use of the margin maximization principle helps in generalizing well to unseen data.
• Versatile. SVMs can be applied to both classification and regression problems. They support different kernel functions, enabling flexibility in capturing complex relationships in the data. This versatility makes SVMs applicable to a wide range of tasks.
• Effective in cases of limited data. SVMs can work well even when the training data set is small. The use of support vectors ensures that only a subset of data points influences the decision boundary, which can be beneficial when data is limited.
• Ability to handle nonlinear data. SVMs can implicitly handle non-linearly separable data by using kernel functions. The kernel trick enables SVMs to transform the input space into a higher-dimensional feature space, making it possible to find linear decision boundaries.

Disadvantages of SVMs

While support vector machines are popular for the reasons listed above, they also come with some limitations and potential issues:

• Computationally intensive. SVMs can be computationally expensive, especially when dealing with large data sets. The training time and memory requirements increase significantly with the number of training samples.
• Sensitive to parameter tuning. SVMs have parameters such as the regularization parameter and the choice of kernel function. The performance of SVMs can be sensitive to these parameter settings. Improper tuning can lead to suboptimal results or longer training times.
• Lack of probabilistic outputs. SVMs provide binary classification outputs and do not directly estimate class probabilities. Additional techniques, such as Platt scaling or cross-validation, are needed to obtain probability estimates.
• Difficulty in interpreting complex models. SVMs can create complex decision boundaries, especially when using nonlinear kernels. This complexity may make it challenging to interpret the model and understand the underlying patterns in the data.
• Scalability issues. SVMs may face scalability issues when applied to extremely large data sets. Training an SVM on millions of samples can become impractical due to memory and computational constraints.

Important support vector machine vocabulary

C parameter

A C parameter is a primary regularization parameter in SVMs. It controls the tradeoff between maximizing the margin and minimizing the misclassification of training data. A smaller C enables more misclassification, while a larger C imposes a stricter margin.

Classification

Classification is about sorting things into different groups or categories based on their characteristics, akin to putting things into labeled boxes. Sorting emails into spam or nonspam categories is an example.

Decision boundary

A decision boundary is an imaginary line or boundary that separates different groups or categories in a data set, placing data sets into different regions. For instance, an email decision boundary might classify an email with over 10 exclamation marks as "spam" and an email with under 10 marks as "not spam."

Grid search

A grid search is a technique used to find the optimal values of hyperparameters in SVMs. It involves systematically searching through a predefined set of hyperparameters and evaluating the performance of the model.

Hyperplane

In n-dimensional space -- that is, a space with many dimensions -- a hyperplane is defined as an (n-1)-dimensional subspace, a flat surface that has one less dimension than the space itself. In a two-dimensional space, its hyperplane would be one-dimensional or a line.

Kernel function

A kernel function is a mathematical function used in the kernel trick to compute the inner product between two data points in the transformed feature space. Common kernel functions include linear, polynomial, Gaussian (RBF) and sigmoid.

Kernel trick

A kernel trick is a technique used to transform low-dimensional data into higher-dimensional data to find a linear decision boundary. It avoids the computational complexity that arises when explicitly mapping the data to a higher dimension.

Margin

The margin is the distance between the decision boundary and the support vectors. An SVM aims to maximize this margin to improve generalization and reduce overfitting.

One-vs-All

One-vs-All, or OvA, is a technique for multiclass classification using SVMs. It trains a binary SVM classifier for each class, treating it as the positive class and all other classes as the negative class.

One-vs-One

One-vs-One, or OvO, is a technique for multiclass classification using SVMs. It trains a binary SVM classifier for each pair of classes and combines predictions to determine the final class.

Regression

Regression is predicting or estimating a numerical value based on other known information. It's similar to making an educated guess based on given patterns or trends. Predicting the price of a house based on its size, location and other features is an example.

Regularization

Regularization is a technique used to prevent overfitting in SVMs. Regularization introduces a penalty term in the objective function, encouraging the algorithm to find a simpler decision boundary rather than fitting the training data perfectly.

Support vector

A support vector is a data point or node lying closest to the decision boundary or hyperplane. These points play a vital role in defining the decision boundary and the margin of separation.

Support vector regression

Support vector regression (SVR) is a variant of SVM used for regression tasks. SVR aims to find an optimal hyperplane that predicts continuous values, while maintaining a margin of tolerance.