What is a qubit (quantum bit)?
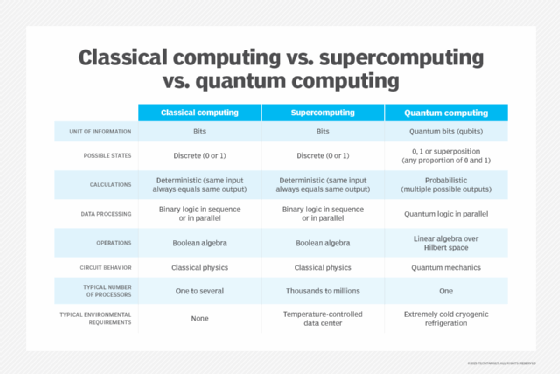
A qubit, short for quantum bit, is the basic unit of information in quantum computing and the counterpart to the bit, or binary digit, in classical computing. A qubit plays a similar role as a bit in terms of storing information, but it behaves much differently because of the quantum properties on which it's based.
In a quantum computer, a number of elemental particles such as electrons or photons can be used (in practice, success has also been achieved with ions), with either their charge or polarization acting as a representation of 0 and/or 1. Each of these particles is known as a qubit; the nature and behavior of these particles, as expressed in quantum theory, form the basis of quantum computing. Two of the most relevant aspects of quantum physics are the principles of superposition and entanglement.
Qubit vs. superposition
When used as a qubit, a particle is placed in a controlled environment that protects it from outside influences. For example, it might be floated in a magnetic field or embedded with specialized circuitry, which is then isolated from the outer environment. In many cases, the entire mechanism is encased in a refrigerated compartment to minimize subatomic disturbances, with temperatures often near absolute zero, or zero kelvins.
Researchers are experimenting with a variety of approaches to creating an environment in which the qubits can be reliably manipulated and measured without being affected by outside factors. For example, one approach is to suspend an electron in an electromagnetic field and control the electron's spin state while isolating the electron from external influences. When the electron's spin is aligned with the field, it is in a spin-up state. When it is opposite to the electromagnetic field, it is in a spin-down state.
The electron's spin can be changed from one state to another by directing a pulse of energy at the particle. The energy might come from a laser beam, microwaves or another source. Each time the pulse is delivered, the electron spin state changes. The switch in state provides a mechanism for assigning a 0 or 1 to each qubit, similar to a bit in classical computing. However, quantum computing makes it possible to do much more with a qubit.
Suppose that the energy pulse delivered to the electron is one unit of energy. What happens if the pulse is only one-half a unit of energy? According to quantum law, the particle enters a state of superposition, behaving as if it were in both the spin-up and spin-down states simultaneously. The electron exists in a fluid state of probability that is mathematically represented by fractions between 0 and 1. It remains in this state until it is observed and measured.

The superposition property enables a quantum computer to be in multiple states at once. The number of possible states grows exponentially as the number of qubits increases. The possible states are represented as 2n, where n is the number of qubits. Figure 2 shows the number of possible states for five different quantities of qubits.
A quantum computer can do much more with its qubits than a classical computer can with the same number of bits. For example, a 2-bit register in a classical computer can store only one of four binary configurations (00, 01, 10 or 11) at any given time. However, a 2-qubit register in a quantum computer can store all four numbers simultaneously, and as more qubits are added, the number of states continues to increase exponentially. To achieve this type of growth, however, quantum computers must also take advantage of another important quantum property: entanglement.
Quantum computing and entanglement
When particles are generated or interact in certain ways, they become entangled -- that is, they retain a connection with each other, even if separated by long distances. As part of this connection, their behavior is correlated across these distances as long as they remain entangled. Quantum computing uses this correlation to achieve the type of exponential growth promised by the superposition state.
When two entangled particles are measured, they are always in opposite spin states because of the correlation between them. When the spin state of one particle changes -- whether from up to down or down to up -- the spin state of the other particle also changes, but in the opposite direction. As a result, knowing the spin state of one entangled particle makes it possible to know the other's spin state.
When an entangled particle is measured, it communicates with the correlated particle, which simultaneously assumes the opposite spin direction. Einstein called this phenomenon "spooky action at a distance," and today's physicists still do not know why it occurs. However, this behavior has been proven through numerous experiments. It is now generally accepted as a given and plays a key role in quantum computing.
Quantum entanglement enables qubits to interact with each other instantaneously. This interaction is not affected by distance or limited to the speed of light. Together with superposition, entanglement makes it possible to greatly enhance computing power and perform calculations in a fraction of the time compared with today's most powerful classical computer.
Quantum computing is still in its infancy. Potential future applications include AI and machine learning, financial modeling, cybersecurity, route and traffic optimization, manufacturing, drug and chemical research, and creation of new materials to be incorporated into products such as batteries and semiconductors.
It is important to be aware of the technical challenges of qubits. Qubits can be sensitive to disturbances in their environment, which can degrade coherence and disrupt the stability of a quantum state. Maintaining control over a qubit state requires precise calibration of hardware and shielding from external interference, all within extremely cold space or isolated environments.
Another challenge lies in building qubits. Building scalable quantum systems involves managing complex quantum information interactions while ensuring error correction across multiple processors or circuits. Each qubit must remain entangled and isolated long enough for algorithms to execute reliably, which pushes the limits of current devices, implementations and control mechanisms.
Types of qubits
Different physical systems are used to contrast qubits, each with different advantages and limitations. The following are the main types of qubits:
- Superconducting qubits. These use electrical currents within superconducting circuits to represent quantum states. They are among the most developed qubit types but require ultralow temperatures and are difficult to scale.
- Trapped-ion qubits. Ions are held in place using electromagnetic fields and manipulated with lasers. Known for high coherence, they are slower to operate but very precise.
- Photonic qubits. These encode information using the polarization or phase of light particles. Photonic systems are effective for communication but face challenges in the implementation of logic gates.
- Topological qubits. This is a theoretical model still under active research, whose qubits are designed to be more resistant to decoherence by encoding information in the global properties of a quantum system.
Future of qubits
The future of qubits lies in solving the fundamental tradeoffs between coherence, control and scalability. Quantum computing is still in development and not yet ready for deployment. Scientists are experimenting with hybrid approaches that combine multiple hardware platforms to create more stable and versatile quantum architectures. There is growing interest in superconducting and neutral atom technologies, which might unlock the potential to operate thousands of qubits in a single quantum processor.
As research progresses, problems related to error correction, entanglement fidelity and quantum information transfer must be addressed. Developing standardized implementations will be key to moving beyond experimental setups into real-world applications. Over time, innovations in materials, control software and algorithm design might push the quantum field toward practical, programmable quantum computers capable of solving world-scale challenges.
Quantum computing advancements can enhance data centers by optimizing supply chains, improving financial modeling, and boosting AI and machine learning capabilities. Explore seven future potential quantum computing uses and the future of quantum computing.