proportional control
What is proportional control?
Proportional control is a control system technology in which the response (output) is proportional to the difference between a setpoint value and the current value of a process variable.
Control systems in many industrial settings and some smart devices use proportional control. It is common in closed-loop control systems where the output must be maintained as close as possible to the desired setpoint.
Proportional control is a type of feedback control in which the desired control, also known as the setpoint (SP), is compared with the actual output. Here, the actual output is the current value of a process variable (PV).
The system compares the two values and then adjusts the response so that it is always proportional to the difference between the SP and the PV. The SP is continuously monitored, and the SP/PV difference generates an error signal that is utilized to perform the proportional control action.
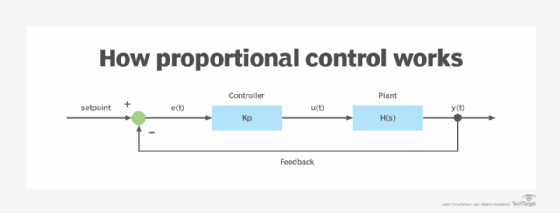
How proportional control works
First, the proportional controller compares the SP value with the actual PV value. Then, the system's feedback loop comes into play. The loop continuously monitors the system output and compares it to the desired output. The inputs are then adjusted to bring the output closer to the desired value.
The controller generates an error signal. Finally, it multiplies the error signal with a multiplication factor to generate an output that is proportional to the error signal and as close to the desired value as possible. The feedback loop ensures that the system can automatically adjust to changes in conditions and maintain a stable output despite internal or external disturbances.
Proportional gain factor and proportional controller output
The multiplication factor used by the proportional controller to generate the output is known as the proportional gain factor. The higher the value of this factor, the faster the control system responds. Conversely, the lower the gain factor, the slower the system's response.
It's important to keep in mind that the output of the proportional controller depends on both the gain factor and the error signal. Thus, if the error signal is zero -- that is, if there is no difference between the SP and actual PV -- then the controller's output is zero, regardless of the gain factor, since multiplying anything with zero yields zero output. If the gain factor is set to too high, the proportional controller behaves like an on-off controller.
Mathematical representation of a proportional controller
The working of a proportional controller can be represented mathematically.
Given the following:
- y(t) = output of the proportional controller
- e(t) = error signal
- K = proportional gain factor
- b = bias signal
Then:
- y(t) = K ⋅ e(t) + b
In the above formula, the output and error signal are variables, while bias is a constant value. Bias is added because it gives a command to the proportional controller when the error signal goes to zero. The command ensures that the controller's output is nonzero.
Example of proportional control
Adaptive cruise control is a well-known example of proportional control. In adaptive cruise control systems, the throttle input is adjusted variably to react to both decreasing slopes and increasing momentum. Furthermore, the throttle of the controlled vehicle is adjusted variably to the proximity of other vehicles in front of it. For emergency collision avoidance, a separate proportional control system acts on the brakes gradually if nearing a followed vehicle too closely or dramatically.
Uses and advantages of proportional control
Proportional control is often used in situations where there is a need to maintain a PV to a tighter tolerance and achieve timely system responsiveness. The latter is possible because proportional control eliminates the cycling time associated with on-off control. A proportional controller is also suitable when the difference between the PV and SP is required to be small and when deviations are not abrupt.
Unlike some other types of control systems, a proportional controller improves system stability since it reduces the steady-state error when the difference between the SP and PV decreases. It also speeds up the response of overdamped systems.
Disadvantages of proportional control
One drawback of a proportional controller is that it produces a steady-state error between the input and output signals. This error is also known as the offset. The offset becomes constant after some time and cannot be eliminated.
Another disadvantage is that both overshoots and undershoots are common in systems with proportional controllers, which may affect performance and output speed. Overshoot refers to the amount by which the system output exceeds the final value in response to some input. Undershoot is the amount by which output falls short of the final desired value.
Proportional control vs. on-off control
On-off control is also known as bang-bang control. In comparison to devices that use on-off control, devices that use proportional control are more complex. Also, proportional control involves fine-grained control through a feedback mechanism. In such systems, the variable response is linearly proportional to the differential between a PV and the desired optimum SP. This means that the response of the controller and the mechanism for affecting the variable make a greater response for a greater differential, as well as a smaller change for a smaller differential.
Additionally, the variability of the response to the PV means tighter tolerances can be maintained in a proportional control system. Proportional control makes processes and production safer and more reliable, especially when automating dangerous machinery, during the handling of sensitive materials and in chemical process systems.
Learn about self-driving cars and how they work, and see how automation brings NetOps to the next level.
