What is impedance?

Impedance vs. resistance

Resistance, denoted as R, is one of the components of impedance. Specifically, it is the real component of impedance. It is a measure of the extent to which a substance opposes the movement of electrons among its atoms, thus resulting in opposition to flowing current within an electrical circuit. The more easily the atoms give up and/or accept electrons, the lower the resistance, which is expressed as a positive real number and expressed in ohms.

Materials with low resistance are known as electrical conductors. As the term suggests, they are good conductors of electricity. Examples include the following:

• Copper.
• Silver.
• Gold.
• Aluminum.

High-resistance substances are poor conductors of electricity and are called insulators or dielectrics. Common insulators include the following:

• Polyethylene.
• Mica.
• Glass.
• Porcelain.
• Rubber.
• Plastic.

Materials with intermediate levels of resistance are classified as semiconductors. Silicon is one of the best-known semiconductors; here are a few others:

• Germanium.
• Gallium arsenide.
• Gallium nitride.
• Indium phosphide.
• Graphene.
• Pyrite.

The phenomenon of resistance is observed with both alternating current (AC) and direct current (DC). That said, impedance is a more useful way to measure the resistance to electrons moving through a substance for AC signals, which tend to be more complex than DC signals, and to measure resistance at specific frequencies. It's also important to note that the resistance and impedance are the same for DC signals.

The basic formula for impedance and resistance is the same: R = V/I and Z = V/I, where V = voltage (volts) and I = current (amperes).

The unit of measurement for both is ohms. However, resistance does not vary by frequency changes. Adding reactance to the impedance formula produces a more advanced formula that takes into account frequency information due to the contributions of capacitance and inductance, which are frequency-dependent. The ability to do so is very useful for certain applications, including audio applications such as audio speakers whose output is affected by their impedance values.

Impedance vs. reactance

Reactance, denoted as X, is an expression of the extent to which an electronic component, circuit or system stores and releases energy as the current and voltage fluctuate with each AC cycle. Simply put, it is the opposition to electrical flow or the resistance observed when sending an AC signal from one device to another.

Like resistance, reactance is also expressed in ohms. But unlike resistance, impedance is only observed for AC signals, not for DC signals. Impedance is expressed as a complex, exponential, imaginary number since it expresses two pieces of information: magnitude and phase in response to a unit current.

When an AC signal passes through a component that contains reactance, energy might be stored and released in the form of a magnetic field. In this case, the reactance is inductive (denoted as +jX_L). Or energy might be stored and released in the form of an electric field, in which case the reactance is capacitive (denoted as -jX_C).

Reactance is conventionally multiplied by the positive square root of -1, which is the unit imaginary number called the j operator, to express Z as a complex number of the form R + jX_L (when the net reactance is inductive) or R - jX_C (when the net reactance is capacitive).

Importance of impedance

In an electrical circuit, impedance represents the extent to which electrical flow is opposed. It is important to know that because the impedance affects the output quality of the circuit and the device that comprises that circuit.

For example, consider audio devices like speakers. If a set of speakers has a higher impedance than the output impedance of the amplifier, the overall resistance is greater so the amplifier will not produce the maximum volume output. To produce this output, the resistance will have to be overcome, which will require more power.

Similarly, headphones with a low impedance will have a lower overall resistance and will therefore produce high-volume output. On the other hand, headphones with higher impedance will require a more powerful signal to produce the same volume output as the low-impedance headphones.

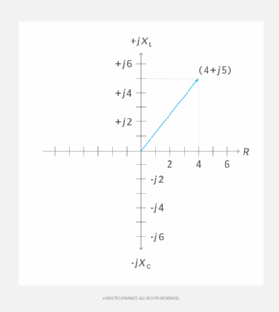
Resistance, reactance, impedance: A visual depiction

The illustration in Figure 1 shows a coordinate plane modified to denote complex-number impedances. Resistance appears on the horizontal axis, moving toward the right. The left half of this coordinate plane is not normally used because negative resistances are not encountered in common practice.

Inductive reactance appears on the positive imaginary axis, moving upward. Capacitive reactance is depicted on the negative imaginary axis, moving downward.

So if R = 4 ohms and Reactance (inductive) = 5 ohms, then Z = 4 + j5.

Here, Z is the complex impedance . It is denoted as a vector from the origin to the point on the plane corresponding to 4 + j5.

Calculating impedance in series circuits

In a series RLC circuit, resistances and reactances add together independently (R = Resistor, L = Inductor and C = Capacitor).

Example 1. A resistance of 100 ohms is connected in a series circuit that includes an inductor. The circuit frequency is 4 MHz. The inductance, measured in Henries (H) is 10 H. Considering these values, here's how the complex impedance of the circuit will be calculated:

Z_RL = R + jX_L = 100.00 ohms + j251.33 ohms

Example 2. Now suppose the circuit includes a capacitor with a capacitance of 0.0010000 Farads (F) instead of the inductor. The resistance is still 100 ohms. The resulting complex impedance at 4 MHz will now be calculated as:

Z_RC = R - jX_C = 100.00 ohms - j39.789 ohms

Example 3. If all three components are connected in series, then the reactances add, yielding a complex impedance of:

Z_RLC = 100 + j251.33 - j39.789 = 100 ohms + j211.5 ohms

This is the equivalent of a 100-ohm resistor in series with an inductor having +j211.5 ohms of reactance.

At 4.0000 MHz, this reactance is presented by an inductance of 8.415 H, as determined by plugging the numbers into the formula for inductive reactance and working backward.

Calculating impedance in parallel circuits

Compared to series RLC circuits, parallel RLC circuits are more complicated to analyze, making it harder to calculate the complex inductance.

To calculate the effects of capacitive and inductive reactance in parallel, the quantities are converted to inductive susceptance and capacitive susceptance, where susceptance is the reciprocal of reactance. Susceptance combines with conductance, which is the reciprocal of resistance, to form complex admittance, which is the reciprocal of complex impedance.

Of course, these are overly simplistic and short explanations of complex concepts. For a deeper understanding of these concepts and how they affect the performance of electrical systems in the real world, further study is recommended using an intermediate electronics text or reference book.

Learn the main factors that can guide your uninterruptible power supply selection process and how to size a UPS unit. See what to know about managing power for edge devices and how to calculate data center cooling requirements.