Erlang C

What is Erlang C?

Erlang C is a traffic modeling formula, primarily used in call center scheduling to calculate delays and to predict waiting times for callers. This mathematical equation enables call centers to predict their load and calculate the number of service/support agents required to service the desired number of calls to achieve a targeted service level.

Erlang C explained

Developed by Danish mathematician A.K. Erlang in 1917, the Erlang C call center traffic model is applicable across many industries and virtual telephony environments. It is widely considered a standard calculation for managing call centers.

With the increasing need among organizations to avoid long waiting times for callers, Erlang C helps estimate the right number of staff or call stations based on the number of incoming calls per hour, average handling time (AHT), average call duration and desired service level. It is a useful means of predicting call center load and forecasting staffing levels.

The Erlang C formula is used when a customer is added to a queue because an assistance resource is not available. The customer then stays in the queue until a resource becomes available. Another Erlang formula is used when a customer is denied service and their request is rejected when they didn't get a free resource. This formula is known as Erlang B.

Erlang C formula

The Erlang C formula provides a way to calculate the probability that a caller waits for an agent, given a particular traffic intensity and the number of available agents.

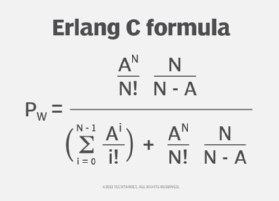
In the accompanying graphic, the various elements are the following:

• P_w = probability of a delay when the customer waits to connect with a support agent, P > 0
• A = total traffic (traffic intensity) of the call center in Erlangs
• N = number of available call center resources/agents

Assumptions in applying the Erlang C formula

The Erlang C formula makes a few assumptions, such as the following:

• The customer requests follow a Poisson arrival process (number of events over a given period of time):
  • The number of customers is large.
  • The impact of a single customer has minimal impact on the overall system performance.
  • All customers use the system independently of others.
• Service times are exponentially distributed.
• Customers never abandon any service request while waiting for a support agent.
• All lost calls are not abandoned, but simply delayed.
• A support agent handles only one customer exclusively for the specified period.
• The total number of support resources is lower than the number of customers.

The Erlang C formula does not work if customer requests are nonindependent or if they're triggered by a common event, such as calling a help line following a natural disaster. Also, the formula usually provides acceptable results only if the number of customers is at least 10 times the number of agents.

How Erlang C is calculated

Although it looks complex, Erlang C is fairly straightforward in its application. Here's how it is calculated:

1. Determine the number of call requests per hour.
2. Compute the traffic intensity:
   1. Calculate call minutes based on AHT (usually in minutes) per request.
   2. Divide call minutes by 60 to compute call hours.
   3. Call hours are the traffic intensity, which is expressed in Erlangs.
3. Identify the number of support agents required to handle the calculated traffic intensity; assume that there's no queuing and every call arrives at the exact moment a previous call is completed.
4. Calculate the probability of nonzero delay (call waiting) by inserting the above computed values into the Erlang C formula.
5. Increase the number of service agents until the desired service level is met.

Manually calculating Erlang C can be cumbersome and time-consuming. However, online calculators and software applications like Excel help simplify the process.

Benefits of Erlang C

Erlang C is a useful formula for all kinds of call centers. It provides a good -- albeit not perfect -- estimate of staffing requirements based on previous or anticipated call load and average call duration. It enables managers to calculate expected load (incoming calls) and make staffing decisions to improve the efficiency and timeliness of operations.

Most callers don't like to be kept waiting. Erlang C provides a mathematical means to ensure staff availability and thus minimize waiting times for customers. Managers can determine a desired service level and then use Erlang C to staff the call center appropriately to minimize queuing, keep costs down and optimize customer experience (CX).

Drawbacks of Erlang C

One drawback of Erlang C is that it assumes that there are no lost calls or busy signals. Consequently, call center managers may end up overestimating staffing requirements.

Another issue is that it doesn't account for fluctuations in the number of calls or available resources during a time period.

Finally, Erlang C makes a few assumptions that don't exactly match with real-world circumstances. For instance, it assumes that lost calls are simply delayed. It also assumes that customers never get a busy signal.

For all these reasons, Erlang C is fairly accurate for good service levels where there are minimal abandoned calls or busy signals. But, when service levels are poor, the formula assumes that the problem is worse than it is.

But, despite these drawbacks, Erlang C is still used for staffing calculations in numerous call centers and workforce management software programs.

See top seven call center agent performance metrics to track, how good CX brings many happy returns on investments, how to manage remote call center agents and how to train agents on call center fraud detection.