What is cryptology?

Basics of cryptology

The terms cryptology and cryptography are often confused or used synonymously, but they are not the same. Cryptology is a broad area that includes cryptography and cryptanalysis. It is derived from two Greek words: kryptós meaning hidden and lógos meaning word.

Cryptography is about creating rules and regulations -- algorithms, protocols and so on -- that are then used to secure data from unauthorized or malicious access. Cryptanalysis is about using methods to break cryptographic security systems in order to recover encrypted messages without knowing the decryption key. Since cryptology incorporates concepts of both cryptography and cryptanalysis, it is a superset of those technologies.

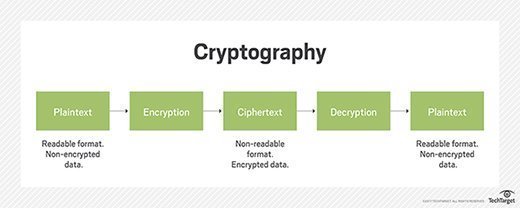
Cryptology is about the scientific study of secure communications and using mathematical equations, frameworks and calculations to create strong security systems that can store data in secure, encrypted (secret) form. For data to be secured for storage or transmission, it must be transformed in such a manner that it is difficult for an unauthorized individual to discover its true meaning. To achieve that, security systems and software use certain mathematical equations that are difficult to solve unless strict criteria are met. The level of difficulty of solving a given equation is known as its intractability. The equations form the basis of cryptography.

Types of cryptology equations

Some of the most important equations used in cryptology are the following.

Discrete logarithm problem

The discrete logarithm problem (DLP) is one of the cornerstones of the fields of cryptology and cryptography. It is described using a finite cyclic group G with a generator g (primitive root modulo p); an element h, where h is an element in the group G and generated by g; and a prime number P, a number that is only divisible by 1 and by itself, and it is concerned with finding an integer x to satisfy the following formula:

g^x = h (mod P)

Simply put, the goal of DLP is to determine the exponent x given a base g, a result h and the modulo P.

The best way to describe DLP is first to show how its inverse concept works. Assume there is a prime number P that is a large prime number of over 300 digits, plus two other integers, a and b. Now, to find the value of N, use the following formula:

N = ab mod P, where 0 ≤ N ≤ (P · 1)

This is known as discrete exponentiation and is quite simple to compute. However, the opposite is true when inverted. Given P, a and N and a requirement to find b so that the equation is valid, then there is a tremendous level of difficulty. This problem forms the basis for a number of public key infrastructure (PKI) algorithms, such as Diffie-Hellman and ElGamal, which is why DLP is considered important in cryptology.

Integer factorization problem

The integer factorization problem is concerned with finding the prime factors of a large composite number. For example, take two prime numbers, P2 and P1, which are both large -- a relative term, the definition of which continues to move forward as computing power increases. Multiply these two primes to produce the product, N.

Thus, the simple formula for the problem is the following:

P1 · P2 = N

The difficulty arises in, given N, trying to find the original P1 and P2.

To simplify matters to a great degree, the N product is the public key, and the P1 and P2 numbers are, together, the private key.

The Rivest-Shamir-Adleman (RSA) PKI encryption protocol is one of the many algorithms based on this problem.

The problem is important for RSA and for other cryptosystems because of the following:

• It assumes that factoring large numbers is computationally infeasible.
• If it can be shown that someone can perform the factoring efficiently, then it can be demonstrated that RSA encryption is insecure.

Other cryptographic algorithms also use the integer factorization problem. Examples include Pollard's rho algorithm, a special-purpose factorization algorithm and Dixon's factorization method, which is a general-purpose integer factorization algorithm.

Elliptic-curve discrete logarithm problem

The elliptic-curve DLP (ECDLP) is a cryptographic protocol based upon a reasonably well-known mathematical problem. It is concerned with reversing scalar multiplication on an elliptic curve E, given a base point P on the curve and an integer k. Another point Q on the curve is the result of multiplying P and k using the curve's point addition operation.

First, imagine a huge piece of paper, on which is printed a series of vertical and horizontal lines. Each line represents an integer, with the vertical lines forming x-class components and horizontal lines forming the y-class components. The intersection of a horizontal and vertical line gives a set of coordinates (x,y). In the highly simplified example below, there is an elliptic curve that is defined by the following equation:

y² + y = x³ · x²

For the above equation, given a definable operator, it is possible to determine any third point on the curve given any two other points. This definable operator forms a group of finite length. To add two points on an elliptic curve, first understand that any straight line that passes through this curve intersects it at precisely three points.

If two of these points are defined as u and v, then draw a straight line through these points to find another intersecting point at w. Then, draw a vertical line through w to find the final intersecting point at x. Now, u + v = x. This rule works for defining another imaginary point, the origin, or O, which exists at theoretically extreme points on the curve. The problem appears to be quite intractable, requiring a shorter key length -- thus, enabling quicker processing time -- for equivalent security levels as compared to the integer factorization problem and DLP.

Mathematicians have studied the properties of elliptic curves for centuries but only began applying them to the field of cryptography with the development of widespread computerized encryption in the 1970s. Today, ECDLP is widely considered the mathematical foundation for the security of elliptic curve cryptography.

Elements of modern cryptology

Today, researchers use cryptology as the basis for encryption in cybersecurity products and systems that protect data and communications. Some of the key elements of cryptology are the following.

Symmetric key cryptography

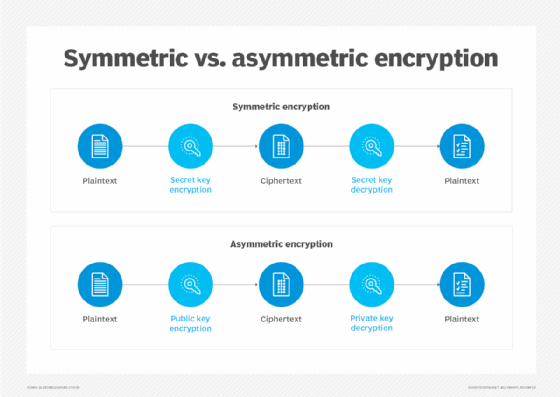
Symmetric key cryptography, sometimes referred to as secret key cryptography, uses the same key to encrypt and decrypt data. Encryption and decryption are inverse operations, meaning the same key can be used for both steps, i.e., to scramble data to make it unreadable and also to unscramble it and make it readable. Symmetric key cryptography's most common form is a shared secret system, in which two parties have a shared piece of information, such as a password or passphrase, that they use as a key to encrypt and decrypt information to send to each other.

Public key cryptography

Public key cryptography, also known as asymmetric cryptography, is a cryptographic approach that involves two separate keys: one private and one public. While both keys are mathematically related to one another, they serve different purposes. The public key, which is not secret, is used by the sender to encrypt the message. The only person who can decrypt the message is the person holding the secret private key, i.e., the authorized recipient. Since the private key is needed to decrypt the message that was originally encrypted with the public key, public key cryptography provides a secure method for communication.

One well-known application of public key cryptography is for digital signatures, which enable users to prove the authenticity of digital messages and documents and make it possible to establish secure communications even over insecure channels.

Cryptanalysis

Cryptanalysis is the practice of analyzing cryptographic systems in order to find flaws and vulnerabilities in them and then use those findings to strengthen the systems. Essentially, cryptanalysis is like penetration testing for cryptographic systems.

For example, cryptanalysts attempt to decrypt ciphertext without knowledge of the encryption key or algorithm used for encryption. They then use their research results to help to improve and strengthen or replace flawed algorithms.

Threat actors also use cryptanalysis methods to break ciphers or cryptographically secured communications. They may use various methods to do this, including the following:

• Known-plaintext analysis, where some known plaintext-ciphertext pairs are mapped to find the encryption key.
• Chosen-plaintext analysis, where the encryption key is determined by obtaining the ciphertext for some random plaintext.
• Man-in-the-middle attacks, where they try to intercept the key by eavesdropping on the communicating parties.

Cryptographic primitives

A cryptographic primitive is a basic cryptographic technique, such as a cipher or hash function, used to construct subsequent cryptographic protocols. Many cryptographic protocols begin by using some basic cryptographic primitives to construct a cryptographic system that is more efficient and more secure and provides stronger data authentication, confidentiality or integrity.

Cryptosystems

Cryptosystems are systems used to encode and decode sensitive information, such as personal or financial data, sent over insecure networks. They incorporate separate algorithms for key generation, encryption and decryption in order to keep data secure. The basic principle of a cryptosystem is the use of ciphertext to transform data held in plaintext into an encrypted message.

How is cryptology used in real life?

One of the most well-known applications of cryptology, specifically cryptography, is data protection. Cryptographic algorithms provide the means to encrypt sensitive data and to maintain its integrity and secrecy. These algorithms are frequently used to encrypt individual files and even larger storage volumes to safeguard the information contained in them from unauthorized access and potentially malicious interception.

Some common use cases of cryptology for data security and/or for maintaining secrecy are the following:

• Electronic banking.
• Other financial transactions, e.g., ATMs and smart credit cards.
• E-commerce.
• Medical databases.
• Legal databases.
• Diplomatic communications.
• Military communications.

Cryptography is also used to create digital signatures that help to verify the authenticity of information sent and received over a digital communication network. Once a document is digitally signed, its recipients can use the sender's public key to verify that the sender is who they are -- their authenticity -- and also to confirm that the information in that document was not illegally modified during its transmission. Digital signatures also facilitate nonrepudiation, meaning a sender cannot deny the validity of a sent message or deny that they sent it. That is an important concept for verifying and ensuring lawfully binding documentation, e.g., contracts.

Another important application of cryptology is in national security. Numerous governments use cryptology to intercept and study electronic signals, also known as signals intelligence. By monitoring foreign electronic traffic, government agencies are able to gain insights into the capabilities, actions and intentions of foreign nations, including their adversaries. This information guides their efforts to ensure the confidentiality, availability, integrity, authentication and nonrepudiation of the telecommunications and information systems vital to national security.

Further explore the differences between symmetric vs. asymmetric encryption, including how they work and common algorithms, as well as their pluses and minuses.