What is the RSA algorithm?

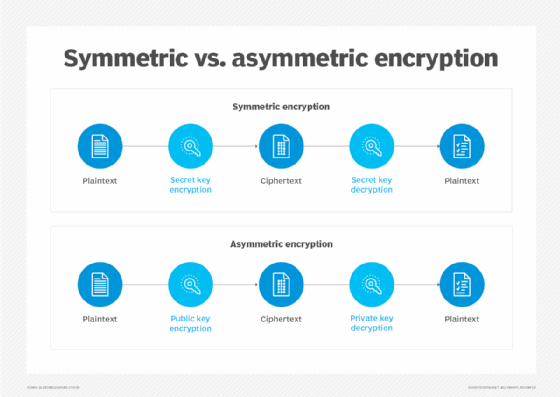
How does the RSA algorithm work?

Use of the RSA algorithm typically consists of four stages: key generation, key distribution, encryption and decryption:

• Key generation. Two large prime numbers are selected and used to generate the public and private keys.
• Key distribution. The public key can be shared with anyone who needs to send encrypted messages to the recipient. The private key is kept secure and only known to the recipient.
• Encryption. To encrypt a message, the sender uses the recipient's public key to transform the message into ciphertext. That makes the message unreadable to anyone who doesn't have the private key.
• Decryption. The recipient uses their private key to decrypt the ciphertext back into the original message. That way, only the intended recipient is able to read the message.

How does RSA key generation work?

RSA is based on the process of factoring large integers. Its security comes from the difficulty of factoring large integers that are the product of two large prime numbers. Multiplying these two numbers is easy but determining the original prime numbers from the total -- or factoring -- is considered infeasible due to the time it would take using even today's supercomputers.

Generating the public and private key pair is the most complex part of RSA cryptography. Two large prime numbers, p and q, are generated using the Rabin-Miller primality test algorithm. A modulus, n, is calculated by multiplying p and q. This number is used by both the public and private keys and provides the link between them. Its length, usually expressed in bits, is called the key length.

The public key consists of the modulus n and a public exponent, e, which is normally set at 65537, as it's a prime number that isn't too large. The e figure doesn't have to be a secretly selected prime number, as the public key is shared with everyone.

The private key consists of the modulus n and the private exponent d, which is calculated using the Extended Euclidean algorithm to find the multiplicative inverse with respect to the totient of n.

How the RSA algorithm is used: An example

The following is an example of the RSA encryption algorithm in action:

• Alice generates her RSA keys by selecting two primes: p=11 and q=13. The modulus is n=p×q=143. The totient is n ϕ(n)=(p−1)x(q−1)=120. She chooses 7 for her RSA public key e and calculates her RSA private key using the Extended Euclidean algorithm, which gives her 103.
• Bob wants to send Alice an encrypted message, M, so he obtains her RSA public key (n, e) which, in this example, is (143, 7). His plaintext message is just the number 9 and is encrypted into ciphertext, C, as follows: M^e mod n = 9⁷ mod 143 = 48 = C.
• When Alice receives Bob's message, she decrypts it by using her RSA private key (d, n) as follows: C^d mod n = 48¹⁰³ mod 143 = 9 = M.

To use RSA keys to digitally sign a message, Alice would need to create a hash -- a message digest of her message to Bob -- encrypt the hash value with her RSA private key, and add the key to the message. Bob can then verify that the message has been sent by Alice and hasn't been altered by decrypting the hash value with her public key. If this value matches the hash of the original message, then only Alice could have sent it, providing authentication and nonrepudiation. A match with the hash also shows that the message is exactly as she wrote it, ensuring integrity.

Alice could provide confidentiality by encrypting her message with Bob's RSA public key before sending it to Bob. A digital certificate contains information that identifies the certificate's owner and also contains the owner's public key. The certificate authority signs the certificates that it issues. Certificates simplify the process of obtaining public keys and verifying the owner.

How secure is RSA?

RSA security relies on the computational difficulty of factoring large integers. As computing power increases and more efficient factoring algorithms are discovered, the ability to factor larger and larger numbers also increases.

Encryption strength is directly tied to key size. Doubling key length delivers an exponential increase in strength. In doing this, though, there is a negative effect on performance. RSA keys used to be 1,024 bits long, but they weren't fully secure against all attacks, and 1,024-bit keys were deprecated in 2013. Since 2013, internet standards and regulatory bodies have banned the use of 1,024-bit keys and advise using RSA keys that are 2,048 bits or longer.

A team of researchers, which included RSA co-inventor Adi Shamir, created a 4,096-bit RSA key using acoustic cryptanalysis. The 4,096-bit keys offer increased data security compared to the 2,048-bit keys, with a slight increase in computational overhead. Security experts have raised concerns that quantum computers will be able to break 2,048-bit RSA keys. The 4,096-bit keys offer greater resistance to such attacks.

However, because of the performance issues, 4,096-bit keys are generally only used in situations where the highest level of security is required. The 2,048-bit keys continue to be the commonly accepted best practice. The National Institute of Standards and Technology deems RSA 2,048-bit keys to be sufficient until 2030.

Barring an unforeseen breakthrough in quantum computing, it will be many years before longer keys are required. Meantime, elliptic curve cryptography is gaining favor with many security experts as an alternative to RSA to implement public key cryptography. ECC can create faster, smaller and more efficient cryptographic keys. For instance, a 256-bit key in ECC delivers approximately the same level of security as a 3,072-bit RSA key.

Modern hardware and software are ECC-ready. It can deliver equivalent security with lower computing power and battery resource use, making it more suitable for mobile apps than RSA. Several cryptocurrencies, such as Bitcoin and Ethereum, already use ECC for key generation and digital signatures.

RSA applications and use cases

RSA has a range of communication and cybersecurity applications. It's compatible with various cryptographic protocols and systems, making it easy to integrate into existing security and communication frameworks.

Common use cases and applications of RSA include the following:

• Secure communications. RSA is widely used to secure communications over the internet, securing the exchange of sensitive information, such as in emails and messaging applications. For instance, RSA encrypts email messages to ensure that only the intended recipients can read them. It can also help establish secure connections between VPN clients and servers, creating a protected tunnel for data transmission.
• Digital certificates. RSA plays a key role in digital certificates, notably SSL/TLS certificates that verify the identity of website owners. These certificates use RSA to encrypt the issuer's digital signature. This signature, along with information about the organization and its domain name, is embedded in the certificate, letting clients trust and securely interact with the website.
• TLS support. RSA is used with the TLS protocol to secure data transmission over the internet. During the TLS handshake, RSA authenticates the parties and establishes a secure connection, enabling safe web browsing and online transactions.
• Secure key exchange. RSA provides secret key exchange, letting two parties share a symmetric encryption key over an insecure channel. The sender encrypts the symmetric key using the recipient's public key. Only the recipient, who holds the corresponding private key, can decrypt and retrieve the shared key, allowing secure communication.
• Financial transactions. RSA safeguards online banking and e-commerce transactions. For example, it protects sensitive financial information, such as credit card numbers and personal data, from unauthorized access during online transactions.
• Software licensing. RSA is also used for software protection to ensure that only authorized users can access or use a particular software product.

Security vulnerabilities and RSA attacks

While RSA is a widely used and trusted cryptographic algorithm, over the years it has had its share of vulnerabilities. Some security concerns associated with RSA include the following:

• Key generation issues. The security of RSA hinges on the randomness of the prime numbers used during key generation. A flawed or predictable random number generator can compromise key security. For instance, if an organization uses a weak random number generator, attackers might be able to discern the pattern used to generate the numbers, thereby facilitating key factorization.
• Compromised keys. If private keys are stolen or compromised, attackers could decrypt encrypted data and impersonate legitimate users.
• Side-channel attacks. These attacks exploit physical information, including timing variations, power consumption and electromagnetic emissions during RSA operations to extract secret information. For example, a side-channel attack can analyze the time taken for certain computations to reveal a private key.
• Fault-based attacks. These attacks purposely introduce faults in the hardware or software implementation of the RSA algorithm to exploit vulnerabilities. For example, attackers might manipulate the power supply or inject electromagnetic radiation and then analyze the resulting errors in the cryptographic computation to extract sensitive information such as private keys.

Here are some past and potential future attacks on RSA:

• Bleichenbacher vulnerability. Discovered in 1998, the Bleichenbacher attack targets the PKCS#1 v1.5 padding scheme in RSA encryption. The padding scheme adds extra data to the plaintext message before encryption to obscure and protect it from potential attacks. The Bleichenbacher vulnerability lets an attacker exploit the deterministic nature of RSA and how padding is handled to decrypt messages. This can enable a practical adaptive chosen ciphertext attack.
• RSA SecurID attack. In March 2011, RSA was targeted by an attack that compromised sensitive data related to its flagship two-factor authentication system, SecurID, now known as the RSA Authenticator. The attack compromised the security of many high-profile organizations that relied on it for access control.
• ROCA vulnerability. The ROCA vulnerability was identified in 2017 and affected RSA key generation in certain hardware security modules. This flaw enabled attackers to factor weak RSA keys generated by specific implementations, making it possible to extract the private key from the public key.
• Quantum computing. Quantum computers pose a significant threat to RSA encryption because Shor's algorithm, which is a powerful quantum algorithm, is able to efficiently factor large numbers. This means that sufficiently powerful quantum computers could quickly break RSA encryption, rendering it ineffective for securing sensitive data.

How to avoid RSA vulnerabilities

If the RSA algorithm is executed without addressing its vulnerabilities, the encryption will be insufficient to withstand attacks and prevent identity breaches. The latest 2025 RSA ID IQ report reveals that identity breaches are more costly than typical incidents, highlighting the importance of strong encryption.

To enhance RSA security and mitigate its vulnerabilities, organizations should consider the following best practices:

• Strong key sizes. Organizations should choose large key sizes of at least 2,048 bits, to make it computationally infeasible for attackers to factor the modulus. For example, larger keys offer a stronger defense against brute-force attacks.
• Strong prime number generation. A strong prime number generator should be used to ensure the prime numbers involved in a key generation are unpredictable and difficult to guess. Small or weak prime numbers can undermine security and should be avoided.
• Tamper-resistant hardware. Organizations should use tamper-resistant hardware to protect against fault-based attacks. For example, hardware security modules isolate cryptographic operations within a physically secure and tamper-resistant environment. This makes it difficult for attackers to introduce faults through physical means such as electromagnetic radiation or power manipulation.
• Padding schemes. To mitigate RSA vulnerabilities, secure padding schemes such as Optimal Asymmetric Encryption Padding should be used. OAEP introduces constant changes to the data encryption process and adds randomness, making it harder for attackers to exploit patterns or weaknesses.
• Vulnerability monitoring. Organizations should stay informed about the latest vulnerabilities and security advisories related to RSA. Regularly reviewing and updating cryptographic libraries and implementations is crucial for addressing any identified weaknesses.
• Alternative algorithms. Given the evolving landscape of cryptography, organizations could consider transitioning to modern algorithms. For instance, ECC offers similar security levels with smaller key sizes and improved efficiency. The Diffie-Hellman algorithm is another alternative that is generally more efficient than RSA in terms of key exchange, especially for quickly establishing a shared secret.

As data volumes and locations expand, strong storage encryption becomes vital for protecting enterprise data. Explore various encryption methods and best practices for securing data.