
Andrea Danti - Fotolia
Comparing Diffie-Hellman vs. RSA key exchange algorithms
See which encryption method uses digital signatures, symmetric key exchanges, bulk encryption and much more in this Diffie-Hellman vs. RSA showdown.
Before delving into which key exchange algorithm is more secure or "better," let me start by explaining the differences between the Diffie-Hellman vs. RSA algorithms.
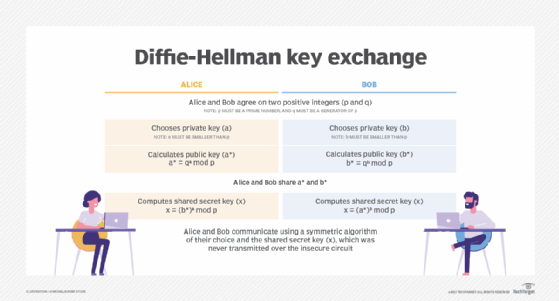
Diffie-Hellman is a key exchange algorithm that allows two parties to establish, over an insecure communications channel, a shared secret key that only the two parties know, even without having shared anything beforehand. The shared key is an asymmetric key, but like all asymmetric encryption key systems, it is inherently slow and impractical for bulk encryption. The key is therefore used to securely exchange a symmetric key, such as AES (Advanced Encryption Standard), which is used to encrypt subsequent communications faster and more efficiently.
The Rivest-Shamir-Adleman, or RSA, algorithm is also an asymmetric cryptographic algorithm that uses two keys: one public and one private. In an RSA key exchange, both the public and private key can encrypt a message, and the opposite key will decrypt it. It is one of the most commonly used key exchanges in computing today.
There are some differences, however. Notably, unlike Diffie-Hellman, the RSA algorithm can be used to sign digital signatures, as well as symmetric key exchanges, but it does require the exchange of a public key beforehand.
Comparing the security of the algorithms
Diffie-Hellman and RSA are both based on supposedly intractable problems: the difficulty of solving discrete logarithm problems. Their common 1,024-bit and 2,048-bit key sizes offer comparable levels of security.
While both have been subjected to scrutiny by mathematicians and cryptographers, given correct implementation, neither is significantly less secure than the other.
Let's look at some of the actual and perceived vulnerabilities of each.
The nature of the Diffie-Hellman key exchange makes it susceptible to man-in-the-middle (MitM) attacks since it doesn't authenticate either party involved in the exchange. In a MitM attack, a third party masquerades as one of the legitimate parties and creates a key pair to spoof messages. Thus, the attacker can encrypt and decrypt messages sent between the two parties. To prevent MitM issues, a means of mutual authentication -- generally, digital signatures -- is critical. Using Diffie-Hellman in conjunction with an algorithm such as Digital Signature Standard can also provide proper authentication.
RSA key exchange vulnerabilities have made headlines, though many issues had to do with its implementation versus the algorithm itself. For example, 2017's ROCA (Return of Coppersmith's Attack) vulnerability was caused by the code of a particular brand of chip and how it implemented key pair generation. The 2017 ROBOT (Return of Bleichenbacher's Oracle Threat) attack, which exploited a vulnerability first discovered in the well-known 1998 Bleichenbacher attack, was connected to servers implementing TLS using an outdated version of RSA Public-Key Cryptography Standards #1 version 1.5 specification. In both attacks, proper and up-to-date use of the algorithm could have prevented issues.

While 1,024-bit keys were considered sufficient until just a few years ago and are still commonly used, NIST recommends using at least 2,048-bit keys, which network security company RSA Security believes will be secure until 2030. However, if security is required beyond 2030, RSA Security recommends using 3,072-bit keys.
Another consideration to note is that RSA doesn't provide perfect forward secrecy (PFS); Diffie-Hellman does. With PFS, unique session keys are created for each exchange session. Should a session become compromised, data from other sessions would remain secure.
When to use Diffie-Hellman vs. RSA
Now that we've established that Diffie-Hellman and RSA can provide the same levels of security, you may be asking which is better to use when. In terms of which is "better," each algorithm has its pros and cons and proper scenarios in which to use it. Most encryption systems offer a choice between the two. For example, SSL 3.0 supports a choice of key exchange algorithms, including the RSA key exchange when certificates are used and the Diffie-Hellman key exchange for exchanging keys without certificates and without prior communication between client and server.
Choosing an encryption key exchange algorithm is largely dependent on interoperability constraints, as well as speed and cost.
Diffie-Hellman is used for data communication but not as commonly for data stored or archived over long periods of time. It is commonly implemented in protocols such as TLS, IPsec, SSH and PGP (Pretty Good Privacy). It is used in PFS thanks to its fast key generation capabilities. Diffie-Hellman is often used to remotely access another computer and send encrypted emails.
Many protocols, including SSH, OpenPGP, S/MIME (Secure/Multipurpose Internet Mail Extensions) and SSL/TLS, use RSA for encryption and digital signature functions. Software programs, including web browsers, use RSA to establish a secure connection over an insecure network, like the internet or corporate WAN, or to validate digital signatures. RSA signature verification is one of the most commonly performed operations in IT systems.
RSA is often used in combination with other encryption schemes or for digital signatures. It is generally not used to encrypt entire messages or files, as it is resource-heavy and less efficient than symmetric key encryption. However, it is often used to encrypt the symmetric key of symmetric key algorithms. In this scenario, only the entity with access to the RSA private key will be able to decrypt the symmetric key.
RSA is used for email, VPNs, chat and communications channels. TLS handshakes often use the RSA algorithm.
Would you ever use Diffie-Hellman and RSA together? It's important to remember that RSA and Diffie-Hellman are independent protocols and do not rely on each other. You can't really merge the two algorithms because of the unique attributes and complexity that each one has. Most encryption systems offer a choice between them rather than combining them.







