Regression in machine learning: A crash course for engineers

What is regression in machine learning?

Regression techniques have become a machine learning staple. ML regression provides an output value based on an input, computed using an algebraic linear regression formula. A linear relationship, such as y=mx+b, results in output y as a function of input x. The value m is the constant or coefficient of the line, such as its rise, or vertical change, over its run, or horizontal change. The b value represents the y-intercept, which is where the line crosses the y-axis.

The critical element of a regression equation is the coefficient m. It represents the best fit of the line to the available data. Advanced forms of regression, such as polynomial regression, use more sophisticated algebraic relationships to model curves other than straight lines.

Regression is a form of supervised ML. This requires the regression-based model to be trained using high-quality, well-documented, highly explainable, carefully tagged, curated data. Once fully trained, the model can produce accurate outputs given its inputs. The actual nature of the input and output data can be anything relevant to the business, such as forecasting the price of a home based on its size.

A business might have to retrain a regression model periodically as the underlying data relationships change. For our home price estimator example, the model might need to be updated as the relationship between house prices and size changes over time.

Regression-based ML models provide value to the business as simple standalone analytical tools, or they can be combined with other algorithms and models to form the foundation of more complex AI platforms. For example, the home price estimator could be combined with other models to build a real estate AI system.

Why is ML regression important to business?

Every business leader wants to make the best, most informed decisions for their group, division and enterprise. Data has always been the foundation of business decisions, but data has traditionally been difficult to obtain, limited in quantity, questionable in quality and challenging to process. This has left data open to interpretation in ways that let leaders succumb to subjective, often flawed, thinking.

The emergence of ML and AI supports objective, data-driven decision-making. Regression algorithms are used to build ML models capable of discovering relationships in large data sets and predicting future outcomes. These models can also recognize potentially valuable or dangerous trends. Consequently, regression has significant business value and can enhance business decisions or actions in the following ways:

• Forecasting trends. Regression can predict trends, such as product demand, sales revenue and the need for routine vehicle maintenance. Forecasting can directly influence business actions, such as strategic planning, budgeting, maintenance and resource allocation.
• Analyzing and optimizing performance. Regression can relate various factors to business outcomes, helping leadership understand the results of business choices. By studying the cause and effect of data and decision-making, leaders can make optimal business decisions.
• Mitigating potential risks. Regression exposes relationships that might indicate potential risks or undesirable outcomes for the business. By spotting potential risks early, leaders can avoid or mitigate them.
• Improve quality. Regression analysis can improve the quality of business products and services. It can also enhance customer satisfaction when interacting with the business. Discoveries made using regression can drive changes to product designs or materials, and prompt changes to business workflows or behaviors.

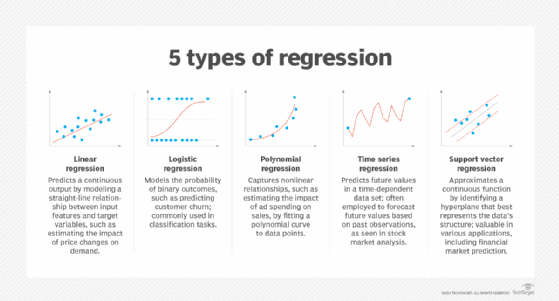
Types of regression and their uses

Regression involves several types of regression algorithms. Each approach has unique characteristics that make it suited to different ML tasks. Common types of regression include the following:

• Linear regression. Linear regression models the relationship between two or more variables. One variable is a dependent variable, and the others are independent variables. The data is related by simply drawing a curve through the best-fit of the data points. Any variable can be determined by knowing the others. This makes linear regression ideal for simply predicting a dependent variable using new production data. Two common variations include simple linear regression with one independent variable and multiple linear regression using two or more independent variables. Linear regression is used for data analysis, data prediction, anomaly detection and trend prediction.
• Logistic regression. This approach models the probability of an event or outcome using a logistic function that maps the output of a linear equation to a probability value between 0 and 1. Logistic regression is suited for yes-or-no outcomes, such as predicting whether an email contains spam. Logistic regression is used in finance, medicine and other industry-specific applications.
• Polynomial regression. This regression model nonlinear relationships between dependent and one or more independent variables using statistical nth degree polynomials. In effect, polynomial regression extends linear regression by allowing the model to fit a curve to the data set rather than a straight line. Each nth degree is a bend in the curve. Polynomial regression is used for complex nonlinear data sets that a straight line can't adequately represent, providing predictive analytics capabilities.
• Ridge regression. Ridge regression is an extension of multiple linear regression for situations where variables are highly correlated, a condition known as multicollinearity. The goal is to improve the best-fit results by reducing regression coefficients to near zero using mathematical relationships derived from calculus. This reduces variations in the model's output, improving reliability and stability, though there's a risk of bias in the resulting relationship.
• Lasso regression. Lasso -- or least absolute shrinkage and selection operator -- regression is another advanced form of linear regression that performs variable selection and coefficient regularization for multiple independent variables. The goal is to shrink less important coefficients to zero, removing irrelevant variables from the model and creating a simpler one. Lasso regression is useful for large data sets with many variables subject to multicollinearity. Lasso regression is used when there are many predictor variables, but only some are important, or when handling complex data in which many variables are correlated.
• Elastic net regression. Elastic net regression creates a more sophisticated model that combines the benefits of ridge and lasso regression. The resulting model can handle multicollinearity and perform variable selection. It does this while preventing overfitting, in which a model becomes so complex that it captures both relevant patterns and inconsequential noise in the training data, leading to inaccurate predictions on new data. Elastic net regression also supports complex data sets and group-correlated data. Elastic net regression often involves several hyperparameters to tune the model and minimize prediction errors.
• Decision tree regression. This type of regression creates a model that uses rules to relate inputs to outputs through a series of internal nodes or decision points. The series of internal nodes that make decisions will lead to leaf or outcome nodes that contain predicted numerical results. Decision trees are suited to nonlinear data and relationships. They are highly explainable but susceptible to overfitting.
• Random forest regression. These regression models use multiple decision trees to aggregate decisions from complex, nonlinear data sets. Random forests can make accurate continuous predictions for target variables while reducing susceptibility to overfitting.
• Support vector regression. SVR uses support vector machine principles to predict output variables. SVR seeks a plane that fits the data with an acceptable margin of error. The model uses support vectors -- data that falls outside of the margin of error. SVR can handle linear and nonlinear regression tasks and is suited for large, complex, nonlinear data sets. It's a supervised ML model that must be trained using a training data set. It can then apply the learned plane to new data.

Pros and cons of ML regression

Regression techniques bring fundamental data analytics to ML and AI systems, and several advantages. Regression also has disadvantages that organizations should consider when selecting ML algorithms. The following are some common advantages of ML regression:

• Accurate. Regression techniques can deliver accurate models and support large data sets.
• Simple. Many forms of regression are straightforward, easy to implement and easily trained, though some regression types, such as SVR, can be computationally demanding.
• Flexible. Regression can readily model complex data relationships. Some forms of regression, such as decision trees, require minimal preprocessing.
• Tolerance for missing data. Some regression types can readily handle missing data.

However, leaders should consider the potential drawbacks of various regression types, such as the following:

• Overfitting. Some regression types, such as decision trees, tend to overfit, making them excellent for known data but less accurate with new, unknown data.
• Computing resources. More sophisticated regression types, such as decision trees and random forests, demand significant computing resources, resulting in higher overhead costs.
• Data sensitivity. Regression models require high-quality data; poor data leads to poor outcomes and forecasts. Some regression types, such as linear regression, are sensitive to irrelevant or outlying data.

Business uses of ML regression

Machine learning regression can be applied to most business units. Some common uses include the following:

• Sales and marketing. Regression relates advertising, pricing and promotional efforts to sales. This enables granular analysis, such as measuring sales against television, radio, web and email campaigns. Similarly, regression can help predict customer lifetime value using factors such as purchasing history, amount of spend, frequency and recency. This helps sales teams formulate customer retention strategies.
• Operations. Regression helps manufacturing teams understand the relationships among time, utilization and downtime for factory equipment. A business can use this data to formulate predictive maintenance schedules to minimize downtime.
• Finance. Regression is used to forecast expenses and plan budgets. It can help business leaders understand how business costs, capital outlays, interest rates for loans and other factors influence revenue and profit. Similarly, regression can be used for tasks such as customer credit scoring and risk-based pricing.
• Human resources. Regression is able to predict employee turnover when gauged against factors such as pay, benefits and job satisfaction.
• Supply chain management. Regression is used to estimate product build and delivery times, using factors such as production volume, demand, vendor distances and inventory levels. Similarly, shipping costs are estimated based on factors such as distance, weight and fuel costs.

Stephen J. Bigelow, senior technology editor at TechTarget, has more than 30 years of technical writing experience in the PC and technology industry.