Explore the impact of quantum computing on cryptography

Quantum computing could impact encryption's efficacy

Much of today's modern cryptography is based on mathematical algorithms used to encrypt data. With quantum computers, attacks on encryption methods that would normally take years could be theoretically done in days with quantum computers. Asymmetric and symmetric encryption types could both be at risk. Many organizations often use encryption types falling into these categories in a variety of data center assets, including storage and networking devices, in addition to areas like secure email and web browsing.

Shor's algorithm poses threats to asymmetric cryptography

Rivest-Shamir-Adleman (RSA) encryption and most public key cryptographies -- also known as asymmetric cryptographies -- are built on the ability to use mathematical algorithms to encrypt data. For example, RSA uses integer factoring with two prime numbers. A public and private key are generated that are mathematically related in public key algorithms, according to IBM. Even with a brute-force attack, it could take years for a classical computer to break encryption methods like RSA.

The security of RSA and other asymmetric algorithms depends on the difficulty of factoring large numbers. Factoring large numbers is the strength of Shor's algorithm. Many public key cryptographies use prime factorization to generate keys, but Shor's algorithm could, in theory, break asymmetric cryptography with quantum computers, given their ability to conduct complex calculations quickly. Quantum computers could carry out decryption without knowing the private key, according to the Technology and Privacy Unit of the European Data Protection Supervisor.

Shor's algorithm could also compromise other encryption schemes, including Diffie-Hellman and elliptic curve cryptography (ECC), with the use of quantum computers.

Grover's algorithm goes after symmetric cryptography

Organizations may also use symmetric cryptography, or secret key cryptography, to encrypt stored data. Examples of symmetric encryption algorithms are Advanced Encryption Standard (AES), Rivest Cipher 4 and Triple Data Encryption Algorithm.

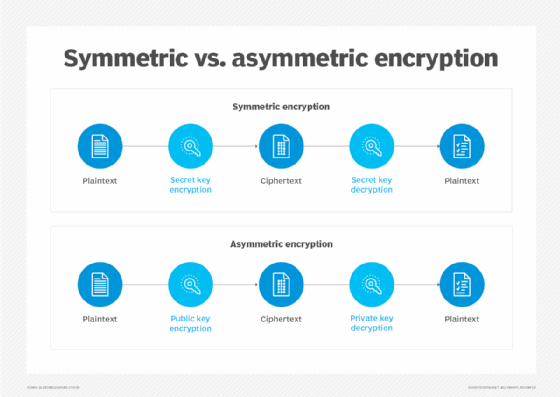
Symmetric encryption converts plaintext into ciphertext and uses a single key for encryption and decryption of data. For example, AES-256 requires a 256-bit key to encrypt and decrypt data. A brute-force attacker would have to guess the key from about 1.1579209 x 10⁷⁷ possible keys, or 2²⁵⁶ keys, according to IT management and services vendor N-able. This makes AES-256 and other similar symmetric encryption algorithms secure.

However, someone sophisticated enough to run Grover's algorithm with quantum computing power could use it to find encryption keys. Grover's algorithm enables someone to conduct searches of large databases much faster than a classical computer. If an algorithm has N, a number of items, Grover's algorithm can search through the list of items and find a specific one in √N steps, according to IBM. This decreases the time it takes to find the key.

Bad actors could also use Grover's algorithm to break hash functions, such as Secure Hash Algorithm 2 and 3, with a quantum computer.

Candidates for post-quantum cryptography and quantum-resistant encryption

There are various options being researched to help hedge against the threat of quantum computing-based attacks on data center infrastructure and data. Many are based on cryptographies that some researchers and experts believe could be quantum-resistant.

Lattice-based cryptography

Lattice cryptography is based on the mathematical concept of lattices and vectors. Most current cryptography follows algebraic problems, but lattice-based cryptography is based on geometrics. Lattice-based computational problems are based on the shortest vector problem, where an attacker must find a point closest to the origin. But, when multiple dimensions are introduced, as opposed to a two-dimensional grid, it is incredibly difficult to solve that problem. Some believe that early quantum computers may be unable to break lattice-based encryption, and it is the most promising option.

Quantum key distribution

Quantum key distribution (QKD) uses quantum mechanics to distribute keys. It relies on the fact that, if you measure a quantum system, it will be disturbed. Therefore, if a malicious actor tries to intercept the key, the parties will know of eavesdropping.

Photons are transmitted over fiber optic cables between parties, where each photon has a random quantum state. When a photon is transmitted and reaches its destination, it goes through a beam splitter and chooses one path or another randomly into a photon collector. Since the receiving party does not know the correct polarization, it then measures the polarization of the photons and shares that information with the sender over another channel. The photons read with the wrong splitter are ignored, and the remaining sequence is used as the key.

QKD is still developing. The National Security Agency, however, said it is only a partial fix for quantum security.

Code-based cryptography

Code cryptography is based on error-correcting codes. It is based on how difficult it is to decode messages that contain random errors where the attacker must recover the code structure. One of the most well-known is the classic McEliece algorithm.

NIST asked cryptographers to begin researching and developing quantum-resistant encryption algorithms for its review and considered McEliece. However, NIST did not standardize it because of its large public key sizes, but it is undergoing further review.

Multivariate-based cryptography

Multivariate cryptography is based on the difficulty of solving systems of equations. It uses a random system of polynomial equations where the recipient must use a private key to perform inverse operations on the generated ciphertext. Even with the encrypted data, attackers would have to solve the equations to read it, which is a difficult computational task.

Isogeny-based cryptography

Isogeny-based cryptography is similar to ECC in that it uses elliptic curves to encrypt data. Instead of relying on the logarithmic problems an ECC method would, isogeny-based cryptography relies on isogenies, or maps between the elliptic curves. Like lattice-based cryptography, these computations could be difficult enough that they would be quantum-resistant.

Other areas organizations are researching for quantum-resistant encryption include zero-knowledge proofs and hash-based cryptographic systems.

How we are preparing for post-quantum cryptography

In 2016, NIST asked cryptographers to begin researching and developing quantum-resistant encryption methods and submit them for review. In 2022, NIST chose four potential quantum-resistant cryptographic algorithms to become part of its post-quantum cryptographic standards, and more are under review.

Three of the algorithms are based on structured lattices, and one uses hash functions, according to NIST. In the fourth round of consideration, NIST will examine four more algorithms. Three are code-based, while the remaining are isogeny-based. Some will be used for general encryption, and others will be used for digital signatures.

While the consensus is that a serious threat from quantum computing on security is many years away, data center admins and security teams shouldn't wait to prepare. Quantum computing security threats likely won't be a problem -- until they are. Security expert Tim Hollebeek said in an interview with TechTarget Editorial that people should look at where they use cryptography in their systems, "what it protects and what are the data protection lifetimes associated" with that data.

Begin working with security teams and stakeholders to prepare systems for a post-quantum world, and plan hardware and software upgrades where needed. Stay up to date with NIST as it reviews post-quantum algorithms, and assess potential options for quantum-resistant encryption.